[低端筆記] MIT算法導論 4. Heaps and Heap Sort

MIT的算法導論公開課有兩種版本, 我選較新版的
MIT 6.006 Introduction to Algorithms, Fall 2011

官方筆記

Heaps and heap sort (PDF)

Priority Queues

一個各元素有其各自權重(key)的set S, 有以下幾種基本操作

• insert(S, x)
• 將元素 x 插入 S 中
• max(S)
• return S 中最大值
• extract_max(S)
• return並移除 S 中最大值
• increase_key(S, x, k)
• 將 x 的權重提高為 k
• Decrease_key(S, x, k)
• 將 x 的權重降為 k

Heap

• Priority Queues的應用
• 為一組array, 可化成一棵nearly complete binary tree
• Max Heap Property
• 根結點 ≥ 子結點
• Min Heap則性質相反

Heap as a Tree

• the root of tree = array的第一個元素, i = 1
• parent(i) = i/2 //父節點
• left(i) = 2i //左子節點
• right(i) = 2i+1 //右子節點
• binary heap 高度為 O(lg n)

Heap Operations 

• build_max_heap
• 從一個unordered array建立Max Heap
• max_heapify
• 將Heap調整成Max Heap(解決不符Max Heap Property部分)
• correct a single violation of the heap property in a subtree at its root
• insert
• extract_max
• heapsort

Max_heapify

1. Assume that the trees rooted at left(i) and right(i) are max-heaps
2. 若 A[i] 不符Max Heap Property, 則向下交換較大值直到符合

Max_heapify(A, i)

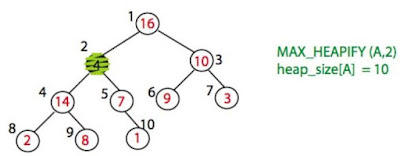A[2]不符, call Max_heapify(A, 2)

A[2]與A[4]互換, A[4]不符, call Max_heapify(A, 4)

A[4]與A[9]互換, 符合Max Heap

複雜度O(log n)

Pseudocode

l = left(i)
r = right(i)
if(l <= heap-size(A) && A[l]>A[i])
  then largest = l
  else largest = i
if(r <= heap-size(A) && A[r]>A[largest])
  then largest = r
if(largest!=i)
  then exchange A[i] and A[largest]
    Max_heapify(A,largest)

build_max_heap

將 A[1...n] 轉換為max heap

Pseudocode

Build_Max_Heap(A):     
  for i=n/2 downto 1
    do Max_Heapify(A, i)

為什麼從n/2開始?

因為A[n/2+1...n]均為leaves → 符合左右子樹均為max-heaps

複雜度:
O(n log n) via simple analysis
實際上為 O(n),
因為leaves上一層節點所需為 O(1), 依此類推, 上l層所需為O(l)
而上一層有n/4個節點, 上上一層有n/8...
→  n/4 (1 c) + n/8 (2 c) + n/16 (3 c) + ... + 1 (lgn c), 設n/4 = 2^k
→  c 2^k( 1/2^0 + 2/2^1 + 3/2^2 + ... (k+1)/2^k )
→  O(n)

Heap-Sort

1. 從unordered array建Max Heap
2. 找出最大元素A[1]
3. Swap elements A[n] and A[1]
• 最大值移至array末端
4. 將node n輸出到sorted array並從Heap移除
• 降低heap-size
5. 跑max_heapify
• 雖然因為A[n]跟A[1]swap可能導致不符特性, 但左右皆為Max Heap, 故只須max_heapify修正
6. Goto #2 直到heap清空